freeCodeCamp/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-144-investigating-multiple-reflections-of-a-laser-beam.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3fc1000cf542c50ff0f	Problema 144: Investigação das várias reflexões de um raio laser	5	301773	problem-144-investigating-multiple-reflections-of-a-laser-beam

--description--

Na física de lasers, uma "célula branca" é um sistema de espelho que atua como uma linha de retardo para o raio laser. O raio entra na célula, colide com os espelhos e, por fim, sai.

A célula branca específica que consideraremos é uma elipse com a equação 4{x}^2 + y^2 = 100

A seção correspondente a -0,01 ≤ x ≤ + 0,01 na parte superior está ausente, permitindo que a luz entre e saia pelo buraco.

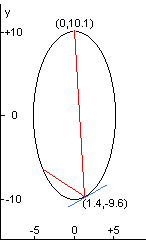
O raio de luz neste problema começa no ponto (0,0, 10,1) no exterior da célula branca e o raio colide no espelho primeiramente em (1,4, -9,6).

Cada vez que o laser atinge a superfície da elipse, segue a lei habitual de reflexão, que diz que "o ângulo de incidência é igual a ângulo de reflexão". Ou seja, tanto o raio incidente como raio refletido têm o mesmo ângulo, com a linha normal no momento da incidência.

Na figura à esquerda, a linha vermelha mostra os dois primeiros pontos de contato entre o raio laser e a parede da célula branca. A linha azul mostra a reta tangente à elipse no ponto da incidência da primeira colisão.

A curva m da reta tangente em qualquer ponto (x, y) da elipse é: m = -4 × \frac{x}{y}

A linha normal é perpendicular a essa reta tangente no ponto de incidência.

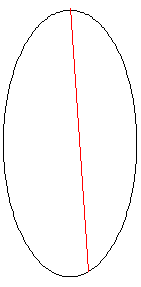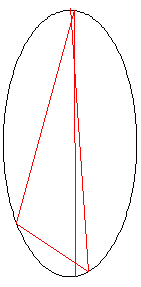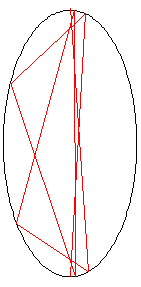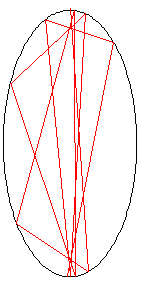
A animação à direita mostra as primeiras 10 reflexões do raio.

Quantas vezes o raio atinge a superfície interna da célula branca antes de sair?

--hints--

laserBeamReflections() deve retornar 354.

assert.strictEqual(laserBeamReflections(), 354);

--seed--

--seed-contents--

function laserBeamReflections() {

  return true;
}

laserBeamReflections();

--solutions--

// solution required